Cut and Restored Checkerboard
Imagine you have a 4x4 checkerboard (alternating black and white squares).

You cut this board into the 16 individual squares, turn them face down, then shuffle them (all the backs are identical). You re-arrange them back into a 4x4 square and turn them over to reveal their faces again.
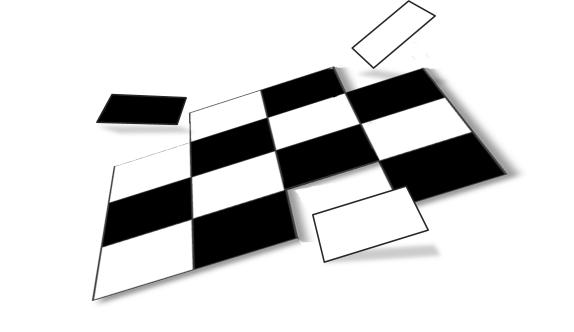
What is the probability that, after the shuffle, the board is back into a checkerboard arrangement? (It does not have to the same chirral version of the checkerboard, the top cornder does not need to be same colour as the original; it can be a rotation, as long as it is well-formed.).
Advertisement:
Solution
Think about turning the squares over one by one. The first square is a gimme, it does not matter what it is, so you have a 100% chance of getting a tile that you need (16/16), then imagine we are walking along each row/column, the first adjacent square needs to be the opposite colour, so there are 8 unpicked opposite tiles from out of 15 unseen (8/15). The next tile reverts to the original color, and there are 7 available out of 14 unseen (7/14), then 7 out of 13 …
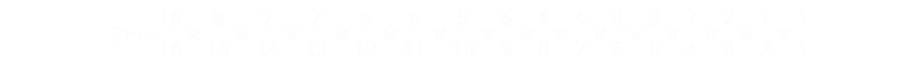
The last tile is a gimme too; there is no choice (1/1).
If you look closely at the top, you will see the numbers come in pairs, and the product of the denominators is just 16!

So you need to repeat the process many thousands of time before expecting to get it right.
Multiple Methods
When I posted this problem to my friends on facebook, many got the correct answer, and there were some different variants in their methods of calculation. Of course, the solution is the same, it just goes to show how there are different ways to skin a cat and a reflection of how different people apply logic in different ways to solve the same problem. Diversity is good.
The most common variant was to chose a color, and make a very similar probability chain, but this time the first term is 8/16 (there are initially eight squares of your selected colour). They then multiplied the entire expansion by two (because there are two possible choices of the first colour).
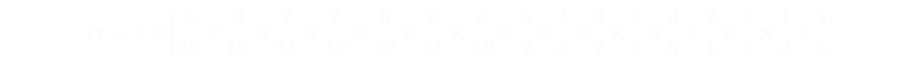
I think you can quickly see this gives the same answer.
Another friend suggested that all we need to is examine eight tiles. Rather than revealing them sequentially, imagine turning them over every other tile (alternating), testing just the squares we hope will be the same colour. If we turn over these eight, and are successful, the remaining tiles have to all be the opposite colour.

Yet another way was to again work with turning over just eight, and say that you had 16 choices for the first pick, the 7 available for the next (you’ve been allocated a colour after the first turn), then 6, then five …
So, there are 16 × 7 × 6 × 5 × 4 × 3 × 2 × 1 variants of picks that all result in the same colour. These eight tiles could be arranged a total of 8! different ways, resulting in a denominator of 16 × 7! × 8! This is the total possible ways the tiles could be arranged so pulled with the first eight appropriate ones of matching colour. There are a total of 16! possible ways all the tiles could be arranged, to the equation is:
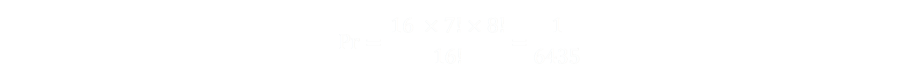
Bigger Grids
Because of the factorials, the numbers get very big very quickly. If you tried this exercise with a larger checkerboard, which is 8x8, you ar4 going to have a pretty miserable time.
| Grid Size | Squares | Probability |
|---|---|---|
| 2 × 2 | 4 | 1 / 3 |
| 4 × 4 | 16 | 1 / 6435 |
| 6 × 6 | 36 | 1 / 453756650 |
| 8 × 8 | 64 | 1 / 916312070471295267 |
| 10 × 10 | 100 | 1 / 50445672272782096667406248628 |
| 20 × 20 | 400 | 1 / 51476250067707216486487940160200993378605462690538824117424529787961666186325979299168297759488246475782024298753387060 |
| 40 × 40 | 1,600 | 1 / 443379162136055359641234343439768180728675811328991809560840985932411616665794610625179716130734073567966685454914526769081922997992544356141257664761375111189515973594333258698627359853661707476667804741933524218116317202661594318938030646740015476156105596539239486989626870695752673594806197985449065125710870301682495128645671569524314271699874701432378162283436054077513804764379973148302054385731110181168513458315363448066603671838507948227740393625045014671786308149987892 |
| 100 × 100 | 10,000 | 1 / 79589513176621947416879863682076059432650291872880727521415955175888631856004789933163142697211110887167929914966131027902316454354010369925439936097979244810208789332292900920497937560344571657989067658702572673659983526069725126923863866800415602689224411975637160877751441590463682322140897729674684450117731440273683141463606610459863401531078919884927624341725423934447497305631011680117649494729464244213795555187160823117601464547772922652011746463893571561989205181296454150037710866527682746212684153140765364826670444627825345437575323807972311188102163426115031339105629687975828557671424122666590534342047642002142349752179628908998215370694711324723793313140931091878770640181273440694272379562978092935734227190930731831175364234105720827732871996642002897085011064345843094689873613943101119894186448801024835509488095308929652913084404058778058898480189904641087427738650602052906745273135799255943306888720770552818471528410362622409715525128243747289814418802147539936457089002650512074670361289879917430105820049272861591548209316844449156072798536234727228325894540967693031283014684158261253135797912117018781396893666443556807176368985646482819033184399068426904617653220698239489907139994902209793987155239444700635985507720608420048172326469764262153355001903348153849628610052213155918266524533756099135006218387226669681935011405896267809407004785986587522489666976138043101786946966488841617188563230751508478074980059754103352945563937822009164001238942785290297135869827808623639851832849309040400982770617878282327782716985397756821058998411741470445746643358523519468079498148772570224854358448059995252621019039383725225431992623152033583510134745628032310291500880650311142378755331283053096885717793609268904810013456908152980878148413938355329732520377383614035737910843509583162129100842946640727470924816609505125163165797180915802977672213340094875675994225646653473295936150510236604360590642305581982082882784466970370488328462939364084203467603657215089362568089007896373557364507915585453585597289149241472082179920329236692353859709329825977666987257173251908808098806308078520177279733387274388706382735739331770709400055981301478667632972843292184860654843491806320282495103962123902677070481534783301535597965784586313401175759104393257773468689819380252321857773976548938325408398500088463329643459378547087558673832874066351770451696727704913659673285654601002064139805794413986423661750898984986281335986413173508878303165652008037775760261659202296378398806122339662097423459696459260226197288837976663434533721596396878047829428216062114261201758329227159852004527348164818181908895779820602502842851345186419030194259856701805814520028316710234470880796912284304385272634695228019441877986607814611383171163395515495602744639679567732072848401065396244397770675371191532646905598743210673954174478278970763499888418917073529519599873945750958181819838795972693767590076249026105225350852754419046772104511227611465010530186185687819294539081693720276824560 |
