Two Swimmers

Two swimmers start at opposite ends of a pool of unknown length. They swim towards each other in parallel lanes. They first meet when they are 84 feet from the left side of the pool. When they each reach the opposite end, they make a perfect turn, and swim back towards their starting side. They cross a second time, this time at 36 feet from the left edge. If each person swims at a constant speed, and there is no time lost in the turns, what is the length of the pool?

It’s clear the swimmers have different constant speeds (otherwise they would have met in the same place, and the solution would be trivial, as this would be halfway).

If the length of the pool is L then, at the first crossing, Swimmer A will have swum 84 feet, and Swimmer B would have swum L–84 feet.

When the pass a second time, Swimmer A will have swum 2L–36 feet (there and almost back; less the 36 feet). Swimmer B will have swum L+36 feet (one length, and 36 feet of the return).

Since the speeds are constant, the ratio of the distances travelled must be constant.

So (ignoring the irrelevant root of L=0), the pool is 144 feet in length.

There’s a more elegant (IMHO) way of looking at this problem that simplifies the math.

At the first crossing point it’s clear to see that the combined distance travelled by both swimmers is one length of the pool.

Similarly, on the second crossing, when they meet they will have, combined, travelled exactly three lengths of the pool.

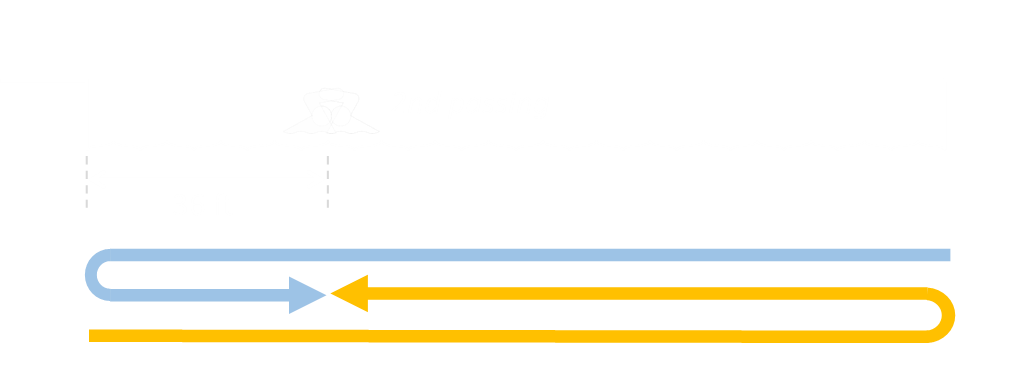
Since the swimmers are travelling with constant speed, then at the second crossing, the total distance travelled by swimmer A is 3 × 84 feet = 252 feet.

This swimmer will have just 36 feet to go to complete two lengths, so the total distance travelled by swimmer A is 252 + 36 = 288 feet.

Since this is two length, a single length is 144 feet. Bingo!