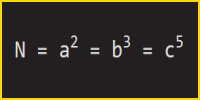Perfect Roots Puzzle

What is the lowest number (other than the trivial answer of one), which is a perfect square, perfect cube, and perfect fifth power?

Specifically what is the lowest N that satisfies the equation:

Where a,b,c are whole numbers.

Interesting piece of trivia: The last digit of any number raised to the fifth power does not change. e.g.:

We could brute force this, but we don’t really know what the range is, plus it seems wasteful when we can apply some simple math to get a solution.

First of all, we want to get all the exponents of all the numbers the same.

We can represent N as some value x raised to the power z. To find a suitable value for z, we can use the lowest common multiple of the powers 2,3,5. As these are all relatively prime, the answer is 30.

Because of the way powers work, we can split this common multiple into the components we need:

Which of course is equivalent to:

We want the lowest value, so after the trivial x = 1, we can insert x = 2, which gives the answer: 1,073,741,824

This answer is quiet a large number because 2,3,5 are relatively prime. If we changed the question to the smaller number with perfect roots for powers of 2,3,6 then the answer would be just 64.