Toilet Paper: How long does it last?

Toilet Paper: How long does it last? (Yes, I did put a colon at the end of Toilet Paper!)

There’s been a lot of hysteria, recently, related to toilet paper; panic buying, and hoarding. If you are reading this, please don’t do it. You’re creating artificial demand, panic, and denying people with genuine need (not to mention distorting demand on a fragile and stressed supply chain).

Toilet paper is typically supplied in rolls of perforated material wrapped around a central cardboard tube. There’s a little variance between manufacturers, but a typical roll is approximately 4.5” wide with an 5.25” external diameter, and a central tube of diameter 1.6”

Toilet paper is big business (see what I did there?) Worldwide, approximately 83 million rolls are produced per day; that’s a staggering 30 billion rolls per year. In the USA, about 7 billion rolls a year are sold, so the average American citizen consumes two dozen rolls a year (two per month).

Again, it depends on the thickness and luxuriousness of the product, but the perforations typically divide the roll into approximately 1,000 sheets (for single-ply), or around 500 sheets (for double-ply). Each sheet is typically 4” long so the length of a (double-ply) toilet roll is approximately 2,000” or 167 feet (or less, if your cat gets to it).

I’ll not get into any vitriolic debates, but there are two, polarized, schools of thought related to how a roll of toilet paper should be mounted on a horizontal dispenser. These are colloquially referred to as over and under mounts.

The choice is a matter of personal preference and familial customs (and I will only comment that statistics suggest that the vast majority of people seem to prefer the over mount).

Because the paper is rolled into a tube, it is essentially stored as a spiral. Also, because of the cardboard core, there’s an offset from the axis. As the roll is consumed the outer radius changes. The shrinkage of the tube is not linear based on consumption. Initially the diameter doesn’t seem to change much, then, as you consume more, it seems to shrink at an ever increasing rate.

I’ve written about this phenonium before when I talked about cassette tapes and reel-to-reel tape decks, but we can take a look again.

Below is a toilet roll. It has width w, thickness t, Length L, outer radius R, and inner radius r.

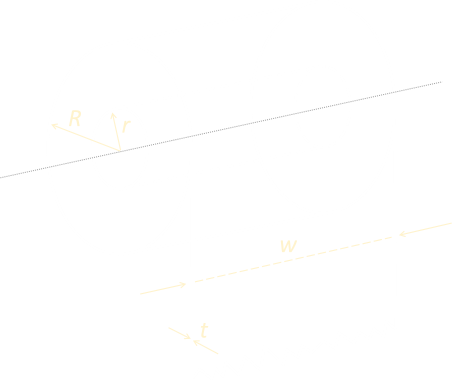
It’s tempting to break out Calculus to work out the relationship between the outer Radius and the current length of paper on the tube, but there’s a simple geometric way. We’re going to use the principle of conservation of Mass. Toilet paper is either on the reel, or it has been consumed.

We’re going to make some assumptions to make this easy. The first is that the part of the roll hanging down (most likely over) is negligible. We’ll also assume the thickness of the paper is negligible compared to the radius of the central tube and that, rather than being an incredibly thin spiral, a roll of paper is just a coaxial plug of paper on the reel.

If we were to take all the paper off the roll, it would make a long strip paper (technically a flat cuboid). The volume of this cuboid is just L × w × t.

This volume of paper should be the same as the coaxial plug of paper on the roll. This gives the formula:

The width cancels, and rearrangement gives an equation for the outer Radius based on the Length of paper:

Plotting this out, we can see how the outer Radius changes as the roll is consumed. On the x-axis is the percentage of the roll consumed (full roll on the left, and empty roll on the right), and on the y-axis is the outer Radius of the roll (measured as a percentage of a full roll). The curve does not go all the way to zero as, when the roll is all consumed, the radius is still that of the cardboard tube.

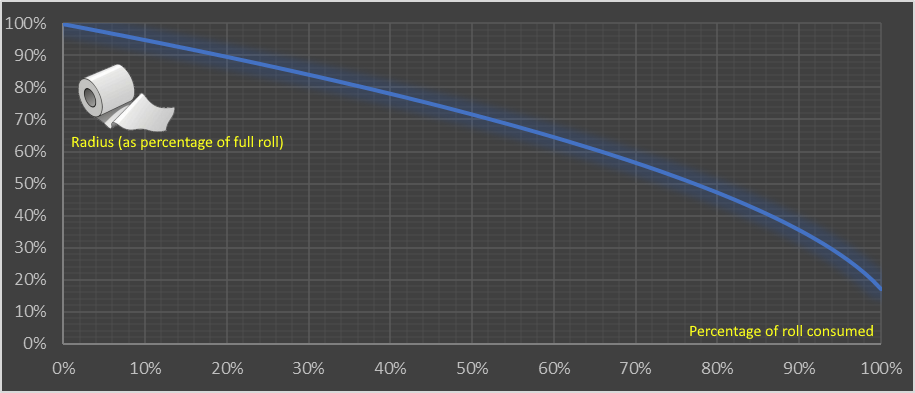
This shows the nonlinear relationship and how the consumption accelerates. The first 10% used makes just a 5% change in the diameter of the roll. The last 10% makes an 18.5% change. The closer you get to the center, the faster it seems to get consumed. Miss-quoting Hemingway from The Sun Also Rises (when Mike is being asked about how he went bankrupt) "Gradually then suddenly"