Blackjack
What’s the probability of being dealt a Blackjack when playing the game of the same name?

A blackjack is made with two cards. One of these has to be an Ace, and the other a 10-point card.
Either the first card is an Ace and the second card is the 10-pointer, or the other way around. There are lots of ways of calculating the correct answer, but I like using a tree diagram:
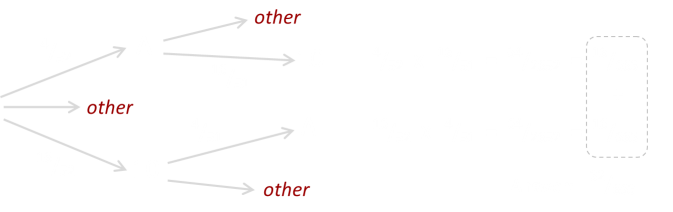
If we are playing with a single deck, then there are only four Aces. However, there are sixteen 10-point cards (4×10, 4×J, 4×Q, 4×K). We can either get dealt an Ace first (4/52), followed by a 10-point card (16/51), or we could be dealt the 10-point card first (16/52), followed by an Ace (4/51). In both cases, on the second probability, the denominator is 51 showing how we've removed one card from the deck. The final probability is the addition (logical OR) of both these paths, and this is 32/663 or approximately 4.827% (close to one time in twenty).
The probability of dealing Blackjack ≈ 4.827%
Two decks
These days, however, casinos don't often use just a single deck. What happens to the probability if they use multiple decks?
At first blush, you might be tempted to think that the odds stay the same (after all, the ratio of the cards stays the same; there is the same proportional number of each card). However, we can see that the odds change because the denominator change is smaller when one card is removed from a larger stack.
Here's the tree diagram for two decks:
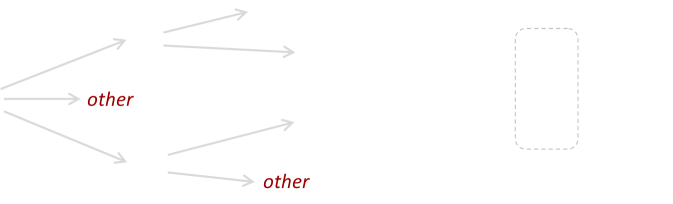
The probability of being dealt a Blackjack has fallen to 64/1339, which is approximately 4.780%
Because of symmetery, the chance of the dealer getting Blackjack also reduces to the same percentage, but on a Blackjack the player gets paid a premium of 3:2 (at a good casino), whilst a dealer only gets even odds (your bet) on a Blackjack. This asymmetry in the payout means that Blackjacks are better for a player than the dealer. Therefore, a lower chance of getting a Blackjack hurts the player more; increasing the house take.
Playing with more decks reduces the chance of a Blackjack – bad for the player!
(The same effect impacts doubling down; another asymmetric advantage to the player. If you are dealt a two card hand of eleven e.g. {6,5}, then you have a slightly higher chance of drawing a 10-point card with a single deck then with a two deck stack).
Advertisement:
More decks
It gets worse the more decks we add. A large shoe at a casino typically holds six decks. Here's a table showing the percentage chance of a Blackjack with an increasing number of decks.
| 1 deck | 4.827% |
| 2 decks | 4.780% |
| 3 decks | 4.764% |
| 4 decks | 4.757% |
| 5 decks | 4.752% |
| 6 decks | 4.749% |
| 10 decks | 4.743% |
| 100 decks | 4.735% |
| 1,000 decks | 4.734% |
The formula for the percentage chance of a Blackjack using d decks is:
At the limit, this reduces the probability to 8/169 ≈ 4.734%
