Pythagoras Revisited

In Euclidean geometry, one of the most well-known theorems is the Pythagorean theorem. It states that, in a right-angle triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

For a right triangle with hypotenuse c, and other sides a, b the equation states:

There are dozens of ways to prove the theorem, but a simple one is a geometric rearrangement.

Starting with a line of length a+b, we can make four copies of this to make a square.

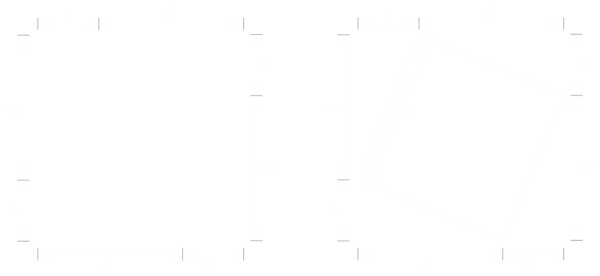
Connecting the points a away from the corners makes another square, internally, with side c. This also forms four right-angle triangles.

This composition can be rearranged to make two rectangles of area ab and the square c². The two configurations are the same total area. A little bit of algebra confirms the theorem.

You've probably seen the formula represented graphically by placing squares on each edge of the triangle. As the area of each square is the edge length squared, there is a simple relationship between the areas of the squares.

There's even some fabulous physical demonstrations of this, as seen in this video:

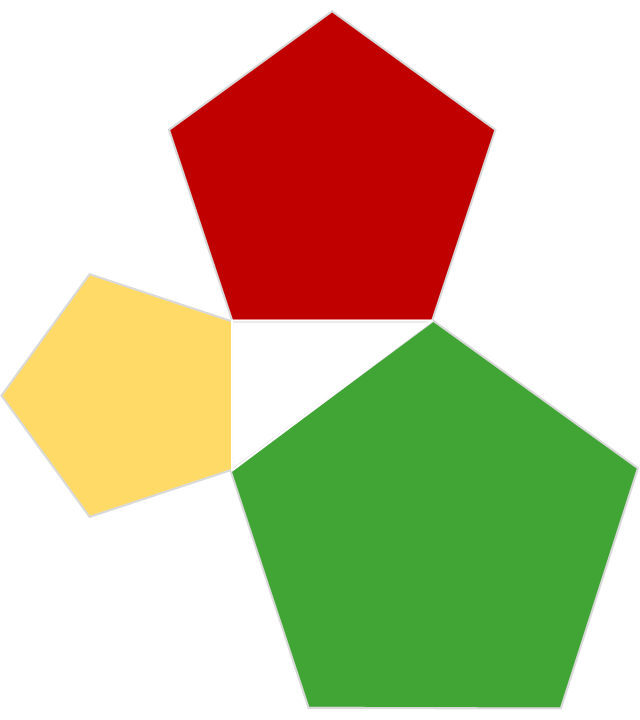
What might blow your mind is that it also works for Pentagons.

Or triangles …

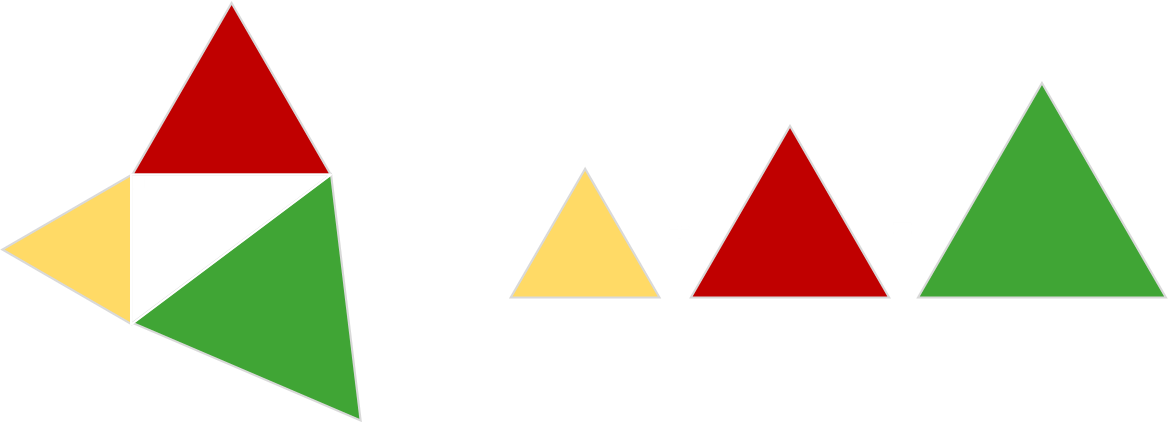
Or any similar shape …

The answer is pretty simple. When you scale up any shape a linear dimension, its area scales up by the square of that change.

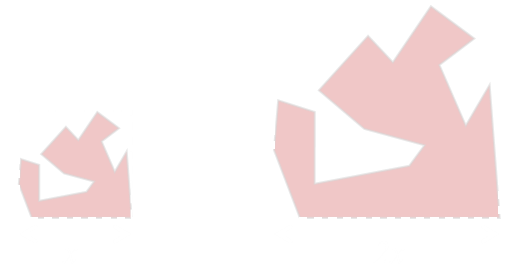
It seems obvious now, when you think about it, but the first time seen it is a surprise to many.

Stay safe.