Ordinal Ranking
In this article I’m going to talk about how to efficiently create a ranking system that orders lists based on the concept of popularity and recency.
I’m sure you’ve encountered these ranking systems many times on the Internet; they have many excellent applications. They are popular on news sites to rank stories, or on bulletin board services to filter 'hot' posts. They are used on games sites to bubble up popular titles, to help surface trending hashtags, to advertise top selling items, and, of course, to order our social media feeds …


The concept is pretty simple; we want to order the list based on popularity of some score (which could be a sales, ranking, rating, up/down votes, players, or some other feedback such as if the article has been read or interacted with).
However, we also want to encourage new and fresh content to appear high up the list, and arrange for the older, staler, content to be slowly moved down to make room for this. Sure, an evergreen article should able to stay high up on the list if it continues to receive a regular cadence of votes or comments, but an article that “supernovas” (burns bright, then fades away) should slide down the list if it does garner any more votes.
What we need is a system that understands the concept of a decaying vote. A vote for any article should provide a ‘boost’ to the total tally for that article, but this individual boost should decay over time. The effect of the boost from a single vote should be fully applied to an article’s score the time it is given, but should be worth slightly less the next day, then slightly more less the next …
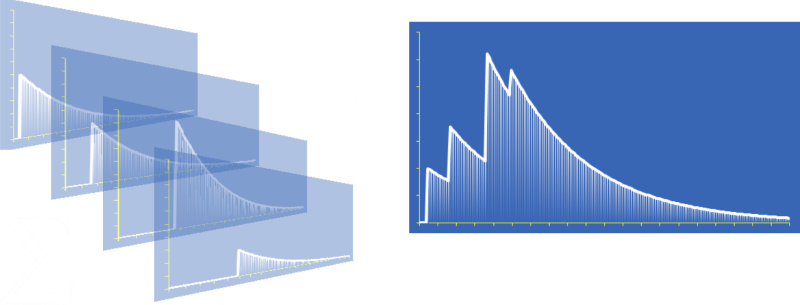
The total score for any article should be the superposition (sum) of all the individual votes cast for that article (each score discounted based on how long it was since it was individually given). The articles can then be ordinarily displayed based on their current total scores.
New articles’ votes will be fresh and help propel the articles up the rank; older articles will need to have been very popular in the past to be near the top, and will still eventually be replaced if they don’t get sufficient votes.
By using the feedback signal (votes) given to an item, its ‘hotness’ relates to how popular it currently is (not based on when it was created). This also allows the article to re-emerge from the ashes, like a phoenix, if it becomes trendy again.
Superposition
The current score for any article should be the sum of all the past votes given, each individually discounted based on the difference in difference in time between when the vote was cast and the current time.
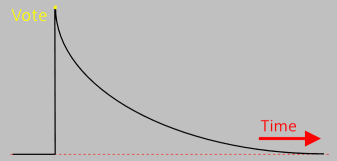
The value of a vote should decay over time.
Decay

There are many ways to model decay, but one that simplifies the math, and mirrors real life is exponential decay. This is sometimes also referred to as Newton's Cooling, radioactive decay, or sometimes half-life decay. As these names imply, these decay curves mimic the way that radioactive isotopes decay, or how objects cool (and also the cross section of temperature gradients in conductors connecting two dissimilar temperatures)*.
The key concept of exponential decay is that the rate of decay is directly proportional to the current value. (The bigger the value, the faster it decays). This can be represented the the simple differential equation below:
Where lambda λ, represents a positive rate constant that defines the rate of the decay.
Separating the variables and integrating gives log result with a constant of integration. By defining N0 at t=0, so N0=eC.
The future value of N can be determined at any time using just the time delta, and the decay constant.
* Exponential Decay can even be used to describe the rate of decay of a head of froth on poured beer.

Half Life
Rates of exponential decay are often quoted, not by using the decay constant λ, but instead by quoting the half-life. This is a time period. It is the time required for the level to decay to half of what it was initially. After two half-lives, the remaining value will be down to a quarter, after three, it will be an eighth …
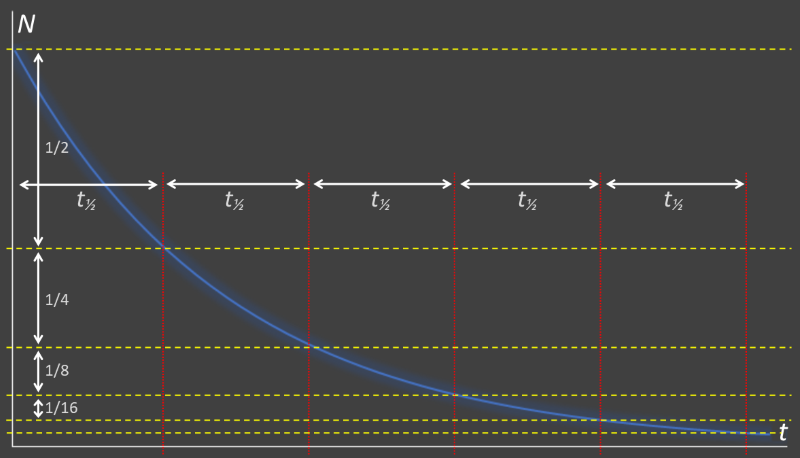
Exponential curves are self-similar. Zooming in to any point results in a similar shaped curve. Any two points of a curve that are at a half-life apart will be at a ratio of 2:1. The relationship between the decay constant and half-life is:
For example, if using days as units, to decay with a half life of a week (7 days) the value of lambda (λ) = 0.0990
Selecting lambda
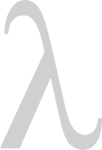
A small value of lambda will give a long half life, and the attenuating effect of the decay will take a long time to be noticeable. The converse happens with a large value of lambda. A site designer should choose this value carefully based the needs of the site and the frequency and volume that votes will be received.
If only a few votes are received a month, having a fast decay will mean that most scores will essentially be zero (unless someone just happened to view the rankings after a vote had been cast). Clearly a compromise needs to be made based on the need.
Another factor should be how often you expect a user to view the rankings. In addition to showing 'top' and 'interesting' content, a good feed displays 'fresh' content (possibly not previously seen). If the cadence that a user is expected to visit your is site just once a week, then you should select the decay constant the reflect this. If they only visit once a year (or every hour), your criterion about what is considered 'fresh' will be different. "Show me the hottest articles this past year" is very different from "Show me the hottest articles in the last hour"
SQL
If your service recorded a vote in a SQL table for each vote with a time stamp and a value, then a naïve way to calculate the current score for an article would be something like this:
SELECT storyid, sum(votevalue * exp(-0.0990 * timestampdiff(SECOND, votetime, now()) / (24*60*60))) FROM votes GROUP BY storyid ORDER BY sum(votevalue * exp(-0.0990 * timestampdiff(SECOND, votetime, now()) / (24*60*60))) DESC
In this example I'm using a value of lambda of 0.0990 to represent a half-life of seven days. The table votes contains a log of every vote cast, a numeric value of this vote, the time the vote was made, and an identifier for the story. This query calculates the current attenuated contribution of each vote, sums these, groups them by story, and finally sorts them.
This certainly works, but is very inefficient. Each time the ranking needs to be updated, the entire votes table needs to be scanned. We can do better.
Better SQL
We can do better by applying the property that exponential decay is a self similar curve. We are agnostic as to where past scores have come from.
If I have $100.00 today, and it decays to $90.57 tomorrow, I don't really care if the $100.00 was received that day, or if it was originally deposited as $110.41 from the day before, or even as $200 from exactly a week ago (or any other combination of past deposits that total $100). All I care about is that there is $100 today (as long as the decay constants are the same).
We can make things much more efficient by creating a new table that simply contains the current running score for each story (only contains one row for each story). Each time the rankings need to be determined, we simply use this query to determine the current values using the last updated score and the time it was taken.
SELECT storyid, score*exp(-0.0990 * timestampdiff(SECOND, lastupdate, now())/(24*60*60)) FROM currentscores ORDER BY score*exp(-0.0990 * timestampdiff(SECOND, lastupdate, now())/(24*60*60)) DESC
We don't actually even need to update the database with the new results of the current scores because they can be correctly calculated at any future time with just a read! (assuming that no other voting has occurred since) This table, containing the cumulative running totals, will be much smaller than the transaction log of all the votes, and much quicker to query.
The only remaining part of our new solution is update this currentscores table when a new vote comes in. When only need to update the row for the storyid in question. We calculate the new current score, add the newvote, and refresh the lastupdate field. Done!
UPDATE currentscores SET score=@newvote + (score*exp(-0.0990 * timestampdiff(SECOND, lastupdate, now())/(24*60*60))), lastupdate=now() WHERE storyid=@votestoryid;
The only time the database is written to is when a vote is cast. After a vote is cast, we never need to recall, individually, what the vote was as it is blended into the current score.
Interactive Demo
Below is an interactive demo using scoring of two fictional stories, one by Alf, and one by Bert.
Using the vote buttons, you can vote for either story with three different values of scores. Each vote is immediately added to the total score, then it starts to degrade. To the right of the names is the current numeric value of the cumulative score and bars representing the individual votes and their contribution to the total.
You can experiment with a high, medium, or low value of lambda (each is an order of magnitude bigger/smaller than the one either side). A high value of lambda gives a short half-life.
Finally, at the bottom is a graph of the rolling sweep of the current scores for the last few seconds. You will notice that, since all votes are using the same lambda that once one author is above another, unless there is more voting, they will never change places.