Self Similarity

This week, it is with great pleasure, that I am publishing a guest post written by one of my readers, Rami Luisto. Rami is a (tall) postdoctoral researcher in mathematics currently working at the University of Jyväskylä. He received his PhD from the University of Helsinki in 2016 and since then he's been spreading his wings at UCLA, JYU and the Charles University in Prague.
In this article, he will explore how to find properties between those of length, area and volume.
Measuring fractals

In this post we are interested in studying the Koch snowflake further, together with other similar objects, by measuring how much 'mass' these objects have. At first glance the question seems almost nonsencial; as the length of the object is infinite but the area is zero the 'mass' must surely be zero of infinity, right? While either of those extremes would be a coherent answer, we can actually do better.
It turns out that, from a certain perspective, the Koch snowflake itself is not a misbehaving object, the problem is just that our measuring tools are too coarse.
Studying the length or area of the Koch snowflake is not unlike trying to calculate the length or volume of a square in the plane: you get weird results because you are not measuring the correct concept, namely, the area of the square.
To properly measure a square we need to find a measure between length and volume, and to properly measure the Koch curve we need to find something between length and area.
Scaling lengths, areas and volumes
Our aim is to find finer properties that lie between length, area and volume. More specifically, if we call length 1-volume, area 2-volume and the 'normal' volume 3-volume, the thing we are trying to define is something like d-volume where d is a number between 1 and 2 (or 2 and 3).
For our approach we need to look at length, area, and volume from the perspective of how they react to scaling i.e. stretching. For simplicity's sake we begin with three objects which are a line segment L of length 1, a square S of side length 1 and a cube C of side length 1.
Now if we take each of these objects and scale them by a factor of two we notice that the length of L doubles, the area of S quadruples and volume of the cube C increases by eightfold.

Similarily we note that if we scale these objects by a factor of 3, the length of L increases by a factor of 3, the area of the square S by a factor of 9 and the volume of the cube C by a factor of 27. We start to notice a familiar pattern emerging:
| Scaling factor: | 2 | 3 | 0.5 | K |
|---|---|---|---|---|
| Length of the line | 2 | 3 | 0.5 | K |
| Area of the square | 4 | 9 | 0.25 | K2 |
| Volume of the cube | 8 | 27 | 0.125 | K3 |
Indeed, we note with very little surprise that scaling an object by a factor of K changes its length by the same factor, its area by the factor of K squared and its volume by K cubed. However, by changing our point of view just a little we can turn this observation into a method of detecting the dimension of an object.
Scaling objects and self-similar parts
When first learning about how scaling affects the length, area and volume of an object, the natural thing to do is to look at how a scaled version of the object breaks into smaller pieces. For our three basic objects we note that when scaled by a factor of two, the line L now contains two copies of the unscaled line, the square S contains four copies of the unscaled square and the cube C eight copies of the unscaled cube.
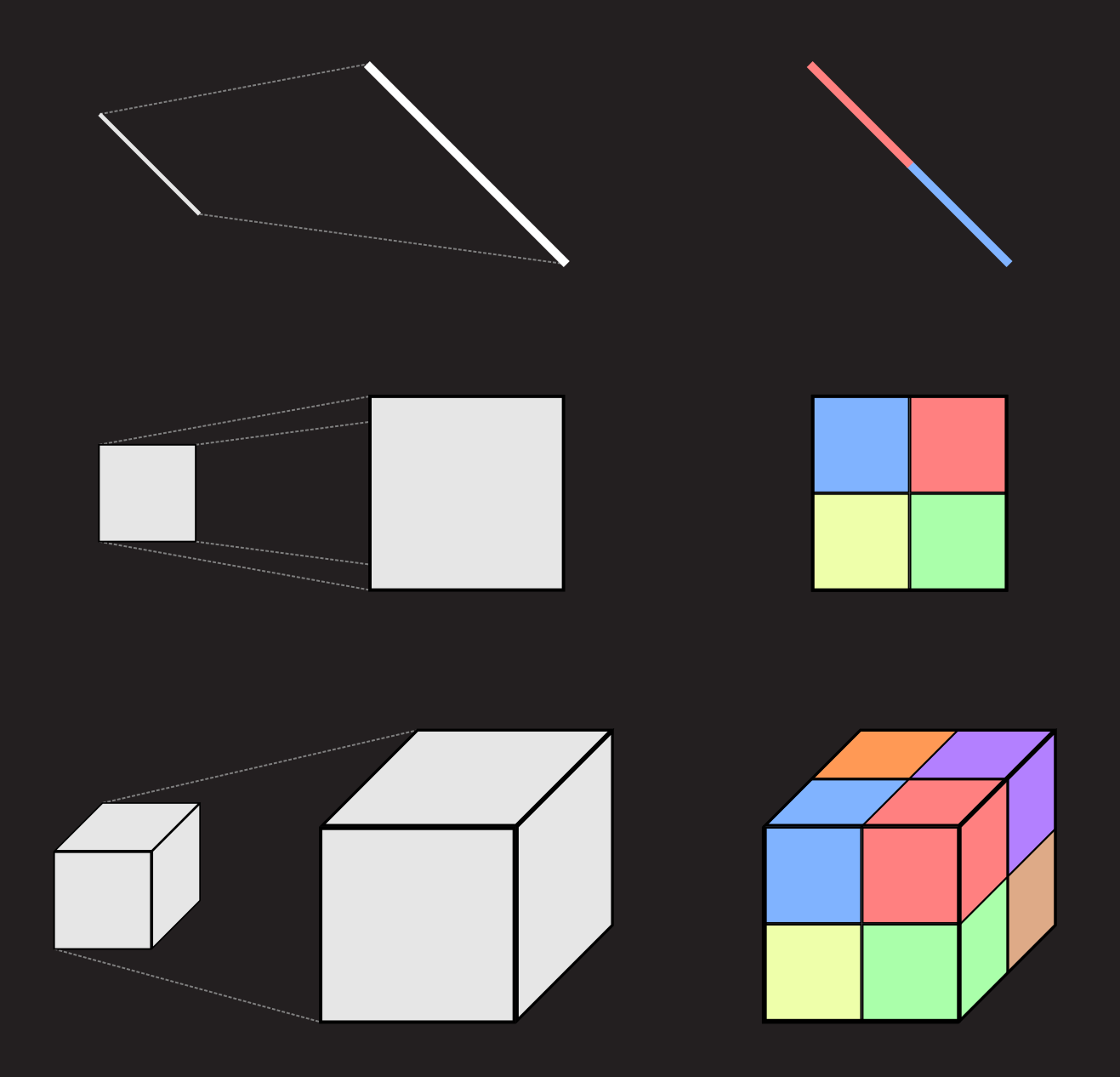
At first glance it might seem that nothing new is gained here, but the important thing is that the statement "when scaled by a factor of 2 the scaled version contains 4 copies of itself" makes no mention of length, area or volume! This means that if you are in a situation where you are uncertain if you should be measuring length, area or volume, you can just try and scale the object with some factor and see if the scaled version is just a collection of some number of copies of the original version.
Note, however, that the factor you need to use might not always be two. For a simple example look at a square with the upper right quarter removed; when scaled by three the resulting shape can be covered with 9 = 32 copies of the original shape, but if scaled by a factor of two the resulting shape cannot be covered by 4 copies of the original. (This is a fun little puzzle to show).
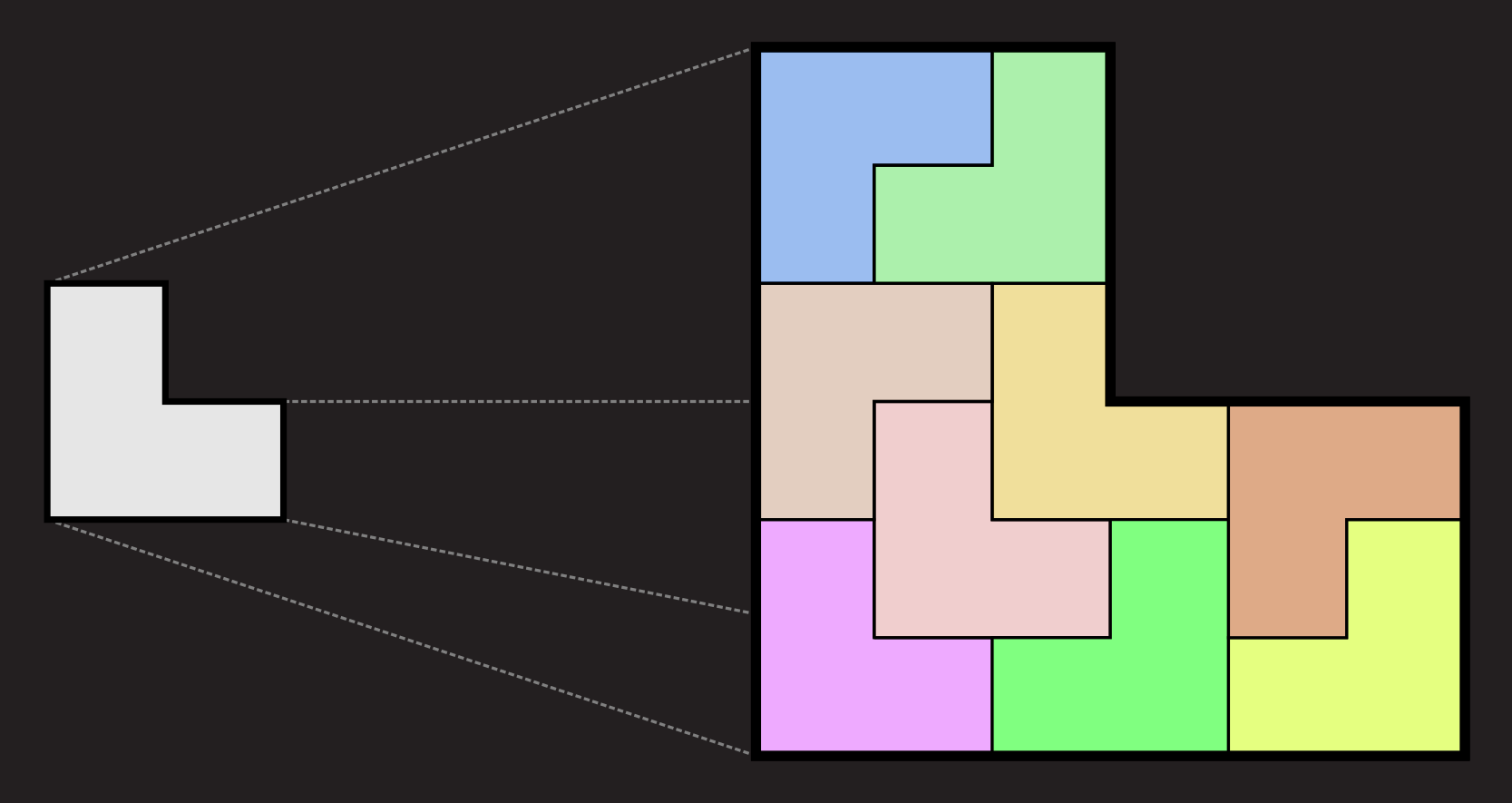
The limitation of not being able to choose the scale freely turns out not to be a problem in the end, and we can formulate our definition of a dimension as follows:
We say that the dimension of a shape A is d, if there exists a number R such that when A is scaled by a factor of R, the resulting shape can be covered with Rd copies of the original shape.
(For those with familiarity with proofs, a fun exercise is to show that if there exists two factors by which the scaling can be done, then the resulting dimensions are the same).
With this definition in hand we can finally start to look for properties that would lie 'between' area and volume. With the definition of a dimension stated above the content of such a property seemes almost natural; we just need to find an object and a number R such that when the object is scaled by a factor of R, the resulting shape can be covered with N copies of the original shape where R2 < N < R3.
Examples with 1<d<2
The first object we study will be the Sierpinski triangle. The Sierpinski triangle is constructed as follows:
- Take an equilateral triangle.
- Divide the triangle to four smaller equilateral triangles and remove the triangle in the center.
- Repeat parts 2-3 for the remaining three triangles.

Note that the consturction is an infinite process, so we cannot actually draw the exact shape except for up to some given precision. This is not as a big as a problem as it might seem at first hand if we compare the situation to that of circles. Any circle we draw will, in the end, consist of a discrete collection of pixels or atoms, and thus is not an actual perfect mathematical circle, but this does not stop us from calculating the area or circumference of a circle. A similar thing holds here, we'll just have to draw approximations and be careful in our reasoning.
By summing up the areas of the removed triangles (this requires some knowledge on how to calculate the sums of geometric series) it is easy to see that the Sierpinski triangle has area of zero. But how does it react to our definition of dimension? We note that if we scale the triangle by a factor of two, we are left with a shape that consists of three copies of the original shape!
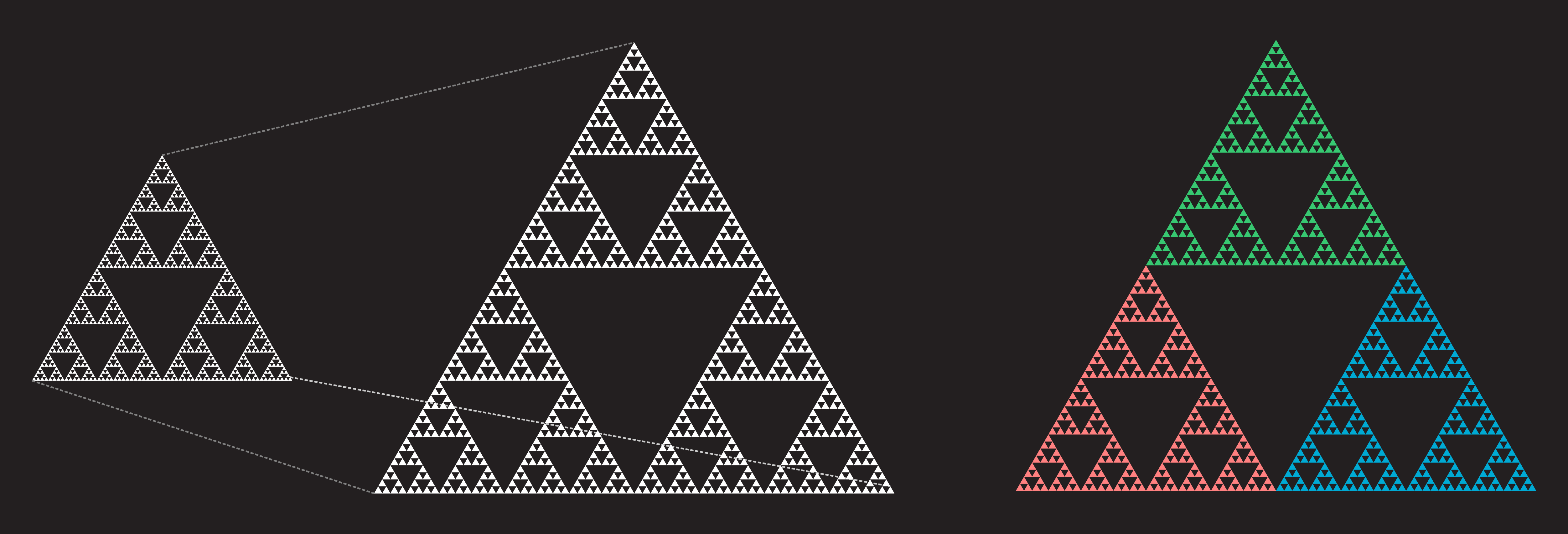
Thus we see that according to our definition the dimension of the Sierpinski triangle is a number d for which 2d = 3. This can be estimated by hand or, if one knows how to use logarithms, calculated to be exactly log(3)/log(2) ≈ 1.585. This means that we have arrived at our first example of an object that seems to have more than length but less than area!
For another classical example, we can look at the Sierpinski Carpet, defined somewhat similarily to the Sierpinski triangle:
- Take an square.
- Divide the square to nine smaller squares and remove the central square.
- Repeat parts 2-3 for all of the remaining squares.

With this shape we notice that scaling by the factor of two does not seem to yield anything, but when scaled by a factor of three we receive a shape consisting of eight copies of the original shape.
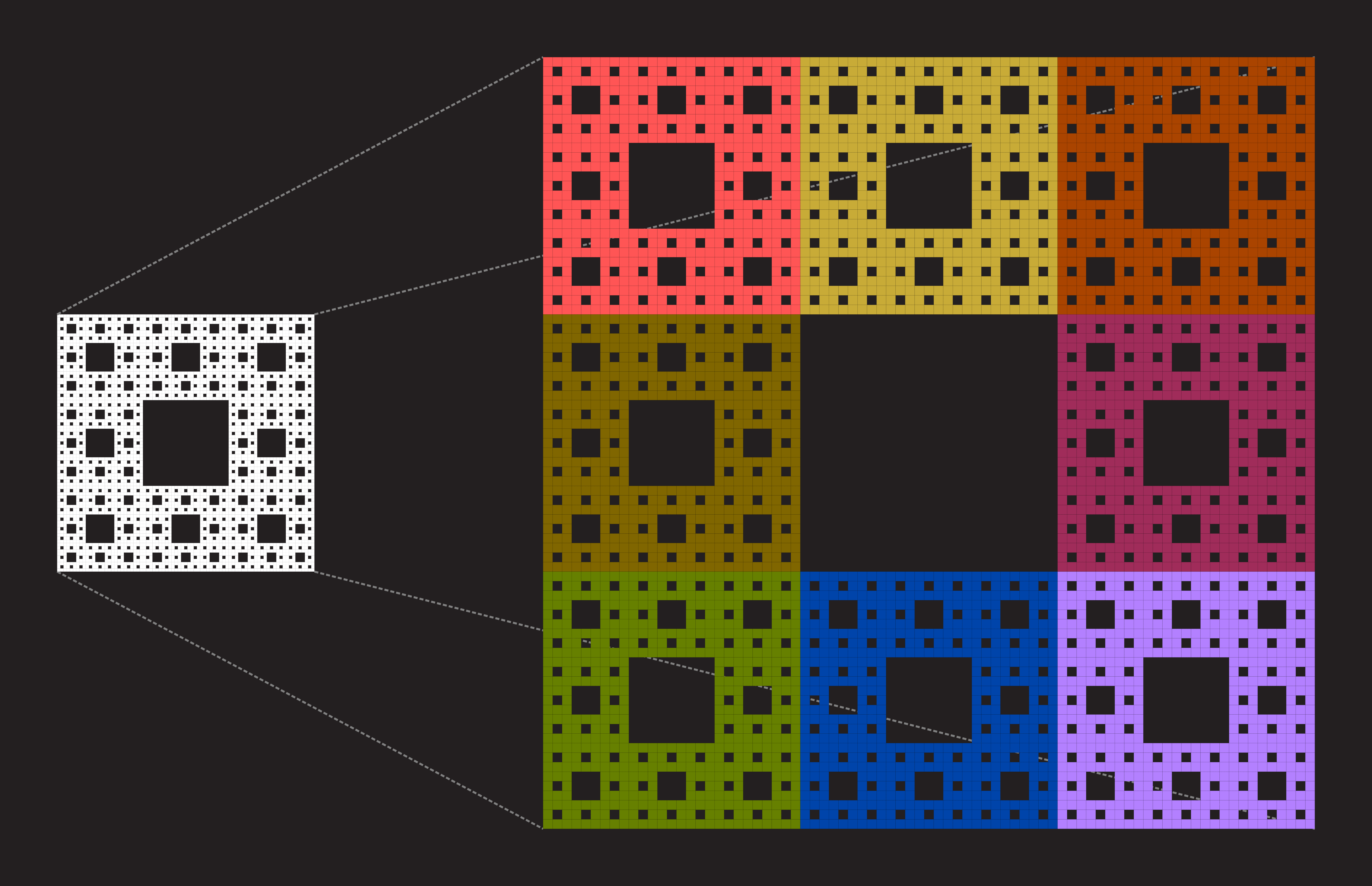
From this we note that since scaling by 3 yields 8 copies, the dimension must be a number d such that 3d = 8. Thus we can again calculate the dimension to be log(8)/log(3) ≈ 1.893.
In particular we note that the Sierpinski carpet has larger dimension than that of the Sierpinski triangle, but both are still strictly between dimensions one and two.
For a third example we revisit the Koch curve from an earlier post and note that if the curve is scaled by a factor of three, the resulting shape consists of four copies of the original shape. The calculation of the dimension is left as an exercise, you can compare your solution to the dimension found from my favorite Wikipedia page discussed below.

Examples with d<1 or d>2
For an example with dimension below 1 we look at a fractal called the Cantor set.
The Cantor set is constucted from a line segment, and the construction follows a familiar pattern:
- Take an line segment.
- Divide the line segment to three smaller segments and remove the middle one.
- Repeat parts 2-3 for the two remaining segments.

The accurate drawing of the Cantor set starts to be a bit difficult, but with the aid of pen and paper we can see that scaling the set by a factor of three yields two copies of the original set. Thus we may once more calculate the dimension of the Cantor set to be log(2)/log(3) ≈ 0.6309.
For our final example we look at the Menger sponge. For this fractal the idea is to start with a cube and divide it into 27 smaller cubes of one third the side length. (Think of a Rubik's cube). We then remove seven cubes: the center-most cube and the six cubes that are in the centers of each of the six sides. We then iterate this process on each of the 20 remaining cubes.
We show here an approximative version of the end result and refer you to Google image search for further imagery.
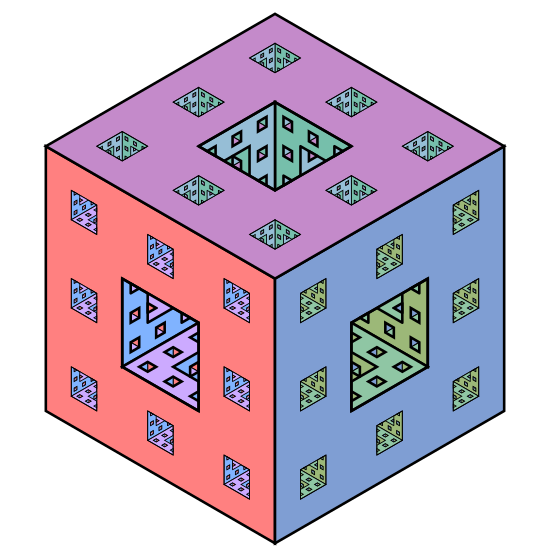
For the Menger sponge we leave the calculation of the dimension as an extra puzzle. You can check your solution from one of my very favorite Wikipedia entries, list of fractals by hausdorff-dimension. From the same page you can find a few further examples by looking for fractals that seem to be self-similar. Note, however, that the definition of a dimension we have used here does not work for most fractals in the list.
What about the actual "volumes" then?
In the beginning I said that we were interested in constructing these new tools between length, area and volume to work with the Koch snowflake and other fractals. At this point it would be natural to tell what is the "1.585-volume" of the Sierpinski triangle, but the answer turns out to be much harder than we might have anticipated!
I had never actually checked what is the exact "1.585-volume" of the Sierpinski triangle, but I had expected it to be the result of some kind of complicated mechanical calculation. Instead it turns out that nobody seems to know! To my best knowledge this is a long-standing open problem in mathematics, and I had not known about it before writing this post. The things you learn.
Some background and further reading
The dimension we defined here is called the self-similarity dimension. It can be used only in the somewhat narrow setting of shapes that consist of smaller copies of themselves; for example we can't use it to calculate the dimension of a ball. When it can be defined it equals the so called Hausdorff dimension of a set which is a more versatile tool but much more complicated to define.
Not counting the basic shapes we used in the beginning, the shapes we studied here were fractals. The term fractal has various not quite equal definitions, but one common requirement is that a fractal should be self-similar, i.e. if scaled up or down it should contain parts that resemble itself. (Another often used property is to require that its Hausdorff-dimension is not an integer.)
All of the fractals here were constructed with a very particular seeming algorithm where we would repeatedly divide an object to smaller parts, remove some of them and iterate on the remaining pieces. Such methods are very useful in constructing the self-similarity that is required in fractals. (But far from being the only methods.) Another related method is that of something called Iterated Function Systems, or IFSs for short. In these we sort of reverse the above process and start to copy and scale down objects to generate fractals. With IFSs it is natural to allow some overlap of the pieces which removes the possibility of using the self-similarity dimension above, but allows for a much wider range of shapes.